accueil › géométrie › angle au centre / angle inscrit
Vocabulaire :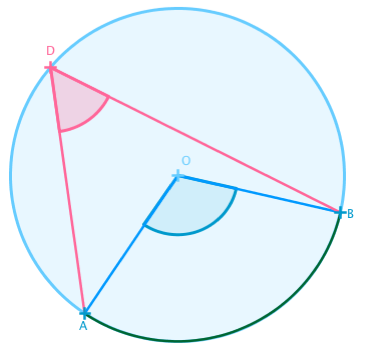
VocabulaiVocabulaiVocabulaiVocabulai
– l’angle à pour sommet un point du cercle et ses côtés coupent le cercle : c’est un angle inscrit dans le cercle.VocabulaiVocabulaiVocabulaiVocabulai
– l’angle a pour sommet le centre du cercle : c’est un angle au centreVocabulai
– les angles et
coupent le même arc de cercle
: ils interceptent le même arc.VocabulaiVocabulaiVocabulaiVocabulai
Il faut savoir reconnaître angles au centre et angles inscrits : exercice 4 du site Mathenpoche
1) Théorème de l’angle au centre eThéorème de l’angle au centreThéorème de l’angle au centre
Observation : Bouge les points de la figure ci-dessous. Que peut-on dire de la mesure d’un angle au centre et de la mesure d’un angle inscrit interceptant le même arc ?
On constate que la mesure d’un angle inscrit est proportionnel à la mesure de l’angle au centre qui intercepte le même arc :
C’est le théorème de l’angle au centre : = 2×
| l’angle au centre mesure le double d’un angle inscrit qui intercepte le même arc |
| Une démonstration en 2 étapes |
2) Théorème de l’angle inscrit
Conséquence du théorème de l’angle au centre (bouge les points ) :
C’est le théorème de l’angle inscrit : =
| 2 angles inscrits qui interceptent le même arc ont même mesure |
3) Un cas particulier du théorème de l’angle au centreUn ca
Bouge le point C: si ce point parcourt le cercle alors le triangle ayant pour côté le diamètre du cercle est TOUJOURS un triangle rectangle !du théorème de l’angle au centre